本文译自 Building Blockchain in Go. Part 2: Proof-of-Work
简介
在前一篇文章中,我们构建了一个非常简单的数据结构,这就是区块链数据库的本质。我们使得可以通过它实现具有链状关系的区块添加:每个区块都与前一个区块相连接。然而,遗憾的是,我们的区块链实现有一个显著的缺陷:向链中添加区块变得轻松而廉价。区块链和比特币的关键之一是添加新区块是一项艰苦的工作。今天我们将修复这个缺陷。
工作量证明
区块链的一个关键理念是,为了将数据放入其中,必须进行一些艰苦的工作。正是这种艰苦的工作使得区块链安全而一致。此外,为这项艰苦的工作支付一定的奖励(这就是人们通过挖矿获得硬币的方式)。
这一机制与现实生活中的机制非常相似:人们必须努力工作以获得奖励,并维持他们的生活。在区块链中,网络的一些参与者(矿工)工作以维持网络,向其中添加新区块,并为他们的工作获得奖励。通过他们的工作,区块以一种安全的方式合并到区块链中,这维护了整个区块链数据库的稳定性。值得注意的是,完成工作的人必须证明这一点。
整个“进行艰苦工作并证明”的机制被称为工作量证明。它之所以困难,是因为它需要大量的计算能力:即使是高性能计算机也无法迅速完成。此外,这项工作的难度会随时间而增加,以保持新区块的产生速率约为每小时6个区块。在比特币中,这项工作的目标是找到一个符合某些要求的区块哈希。而这个哈希就是作为证明的依据。因此,找到证明就是实际的工作。
最后需要注意的一点是,工作量证明算法必须满足一个要求:做工作是困难的,但验证证明是容易的。通常,证明会交给其他人,因此对于他们来说,验证这个证明不应该花费太多时间。
哈希
在这一段中,我们将讨论哈希。如果您对这个概念熟悉,可以跳过这部分内容。
哈希是获取指定数据的哈希值的过程。哈希是对计算的数据的唯一表示。哈希函数是一个接受任意大小的数据并生成固定大小哈希值的函数。以下是哈希的一些关键特点:
- 无法从哈希还原出原始数据。因此,哈希不是加密。
- 特定的数据只能有一个哈希值,且哈希是唯一的。
- 即使在输入数据中更改一个字节,也会导致完全不同的哈希值。
哈希函数广泛用于检查数据的一致性。一些软件提供商除了软件包之外,还会发布校验和。下载文件后,您可以将其输入到哈希函数中,并将生成的哈希与软件开发者提供的哈希进行比较。
在区块链中,哈希用于保证区块的一致性。哈希算法的输入数据包含前一区块的哈希,因此几乎不可能(或至少相当困难)修改链中的一个区块:必须重新计算其哈希和其后所有区块的哈希。
Hashcash
比特币使用Hashcash,这是一种最初用于防止电子邮件垃圾的工作量证明算法。它可以分为以下步骤:
- 获取一些公开已知的数据(在电子邮件的情况下,是接收方的电子邮件地址;在比特币的情况下,是区块头)。
- 向其添加一个计数器。计数器从0开始。
- 获取数据+计数器组合的哈希值。
- 检查哈希是否符合特定的要求。
- 如果符合要求,任务完成。
- 如果不符合要求,增加计数器,然后重复步骤3和4。
因此,这是一种穷举算法:更改计数器,计算新的哈希,检查它,增加计数器,计算哈希,依此类推。这就是为什么它在计算上是昂贵的原因。
现在让我们更详细地看看哈希必须满足的要求。在原始的Hashcash实现中,要求是“哈希的前20位必须为零”。在比特币中,由于设计上每10分钟必须生成一个区块,因此要求会随时间调整,尽管计算能力随着时间的推移增加,越来越多的矿工加入网络。
为了演示这个算法,我使用了前面例子中的数据(“I like donuts”)并找到了一个以3个零字节开头的哈希值:
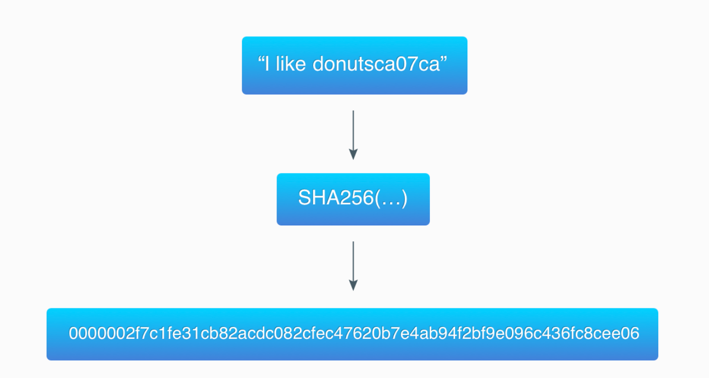
ca07ca是计数器的十六进制值,十进制为13240266。
执行
好了,理论讲完了,让我们来写代码吧!首先我们定义一下挖矿难度:
在比特币中,“targetBits”是存储区块挖掘难度的区块头。目前我们不会实现一个自动调整目标的算法,所以我们可以将难度定义为一个全局常量。
24是一个任意的数字,我们的目标是拥有一个在内存中占用少于256位的目标。我们希望差异足够显著,但不要太大,因为差异越大,找到合适的哈希就越困难。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
type ProofOfWork struct {
block *Block
target *big.Int
}
func NewProofOfWork(b *Block) *ProofOfWork {
target := big.NewInt(1)
target.Lsh(target, uint(256-targetBits))
pow := &ProofOfWork{b, target}
return pow
}
|
在这里创建ProofOfWork结构,它包含对一个block和一个target的指针。在这里,“target”是前面段落中描述的要求的另一个名称。我们使用大整数是因为我们将如何将哈希与目标进行比较:我们将哈希转换为大整数并检查它是否小于目标。
在NewProofOfWork函数中,我们使用值为1的big.Int,并将其左移256 - targetBits位。256是SHA-256哈希的位长度,而我们将使用SHA-256哈希算法。目标的十六进制表示是:
0x10000000000000000000000000000000000000000000000000000000000
它在内存中占用29字节。以下是它与前面示例中的哈希的视觉比较:
1
2
3
|
0fac49161af82ed938add1d8725835cc123a1a87b1b196488360e58d4bfb51e3
0000010000000000000000000000000000000000000000000000000000000000
0000008b0f41ec78bab747864db66bcb9fb89920ee75f43fdaaeb5544f7f76ca
|
第一个哈希(对“I like donuts”进行计算)大于目标,因此它不是有效的工作证明。第二个哈希(对“I like donutsca07ca”进行计算)小于目标,因此它是有效的证明。
您可以将目标看作是范围的上限:如果一个数字(一个哈希)小于这个上限,它就是有效的,反之亦然。降低上限将导致更少的有效数字,因此需要更多的工作来找到一个有效数字。
现在,我们需要准备要进行哈希的数据:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
func (pow *ProofOfWork) prepareData(nonce int) []byte {
data := bytes.Join(
[][]byte{
pow.block.PrevBlockHash,
pow.block.Data,
IntToHex(pow.block.Timestamp),
IntToHex(int64(targetBits)),
IntToHex(int64(nonce)),
},
[]byte{},
)
return data
}
|
这一部分很简单:我们只需将区块字段与目标和nonce合并。这里的nonce是上面Hashcash描述中的计数器,这是一个密码学术语。
好的,所有准备工作都已完成,让我们来实现PoW算法的核心部分:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func (pow *ProofOfWork) Run() (int, []byte) {
var hashInt big.Int
var hash [32]byte
nonce := 0
fmt.Printf("Mining the block containing \"%s\"\n", pow.block.Data)
for nonce < maxNonce {
data := pow.prepareData(nonce)
hash = sha256.Sum256(data)
fmt.Printf("\r%x", hash)
hashInt.SetBytes(hash[:])
if hashInt.Cmp(pow.target) == -1 {
break
} else {
nonce++
}
}
fmt.Print("\n\n")
return nonce, hash[:]
}
|
首先,我们初始化变量:hashInt是哈希的整数表示;nonce是计数器。接下来,我们运行一个“无限”循环:它受maxNonce的限制,maxNonce等于math.MaxInt64;这样做是为了避免nonce可能发生的溢出。尽管我们的PoW实现的难度对于计数器溢出来说太低了,但仍然最好进行这个检查,以防万一。
在循环中,我们:
- 准备数据。
- 使用SHA-256对其进行哈希。
- 将哈希转换为大整数。
- 将整数与目标进行比较。
正如之前解释的那样简单。现在我们可以删除Block的SetHash方法并修改NewBlock函数:
1
2
3
4
5
6
7
8
9
10
|
func NewBlock(data string, prevBlockHash []byte) *Block {
block := &Block{time.Now().Unix(), []byte(data), prevBlockHash, []byte{}, 0}
pow := NewProofOfWork(block)
nonce, hash := pow.Run()
block.Hash = hash[:]
block.Nonce = nonce
return block
}
|
在这里您可以看到随机数被保存为块属性。这是必要的,因为需要随机数来验证证明。块结构现在看起来像这样:
1
2
3
4
5
6
7
|
type Block struct {
Timestamp int64
Data []byte
PrevBlockHash []byte
Hash []byte
Nonce int
}
|
好吧!让我们运行该程序看看一切是否正常:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
Mining the block containing "Genesis Block"
00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Mining the block containing "Send 1 BTC to Ivan"
00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Mining the block containing "Send 2 more BTC to Ivan"
000000b33185e927c9a989cc7d5aaaed739c56dad9fd9361dea558b9bfaf5fbe
Prev. hash:
Data: Genesis Block
Hash: 00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Prev. hash: 00000041662c5fc2883535dc19ba8a33ac993b535da9899e593ff98e1eda56a1
Data: Send 1 BTC to Ivan
Hash: 00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Prev. hash: 00000077a856e697c69833d9effb6bdad54c730a98d674f73c0b30020cc82804
Data: Send 2 more BTC to Ivan
Hash: 000000b33185e927c9a989cc7d5aaaed739c56dad9fd9361dea558b9bfaf5fbe
|
耶!您可以看到现在每个哈希值都以三个零字节开头,并且需要一些时间才能获取这些哈希值。
还有一件事要做:让我们能够验证工作量证明。
1
2
3
4
5
6
7
8
9
10
11
|
func (pow *ProofOfWork) Validate() bool {
var hashInt big.Int
data := pow.prepareData(pow.block.Nonce)
hash := sha256.Sum256(data)
hashInt.SetBytes(hash[:])
isValid := hashInt.Cmp(pow.target) == -1
return isValid
}
|
这就是我们需要保存的随机数的地方。
让我们再检查一次是否一切正常:
输出:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
Prev. hash:
Data: Genesis Block
Hash: 00000093253acb814afb942e652a84a8f245069a67b5eaa709df8ac612075038
PoW: true
Prev. hash: 00000093253acb814afb942e652a84a8f245069a67b5eaa709df8ac612075038
Data: Send 1 BTC to Ivan
Hash: 0000003eeb3743ee42020e4a15262fd110a72823d804ce8e49643b5fd9d1062b
PoW: true
Prev. hash: 0000003eeb3743ee42020e4a15262fd110a72823d804ce8e49643b5fd9d1062b
Data: Send 2 more BTC to Ivan
Hash: 000000e42afddf57a3daa11b43b2e0923f23e894f96d1f24bfd9b8d2d494c57a
PoW: true
|
结论
我们的区块链离实际架构更近了一步:现在添加区块需要进行艰苦工作,因此挖矿成为可能。但它仍然缺少一些关键功能:区块链数据库不是持久化的,没有钱包、地址、交易,也没有共识机制。所有这些内容我们将在未来的文章中实现,目前祝您挖矿愉快!

